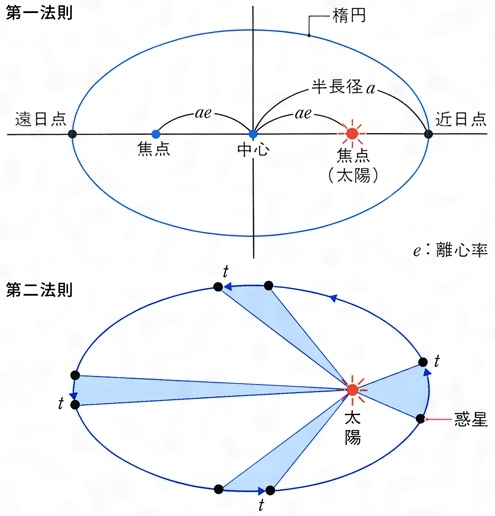
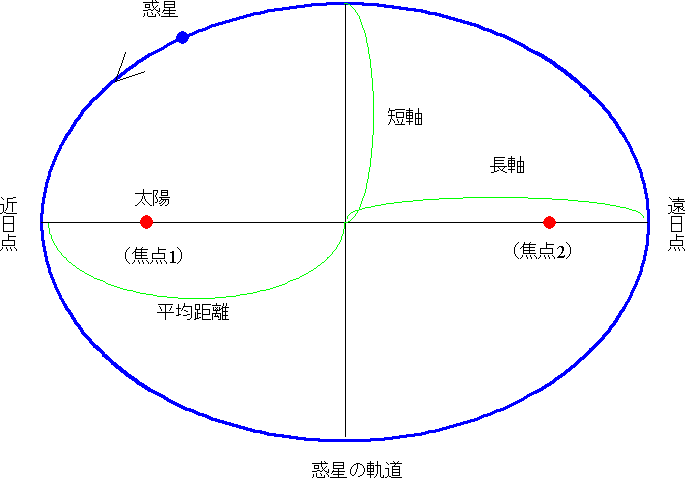
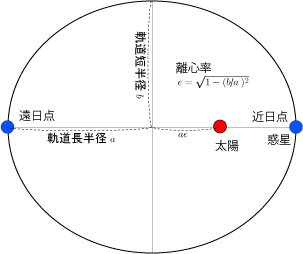
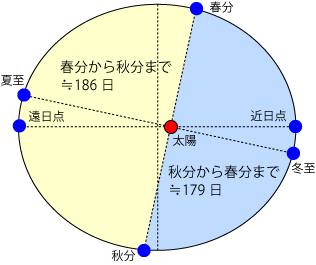
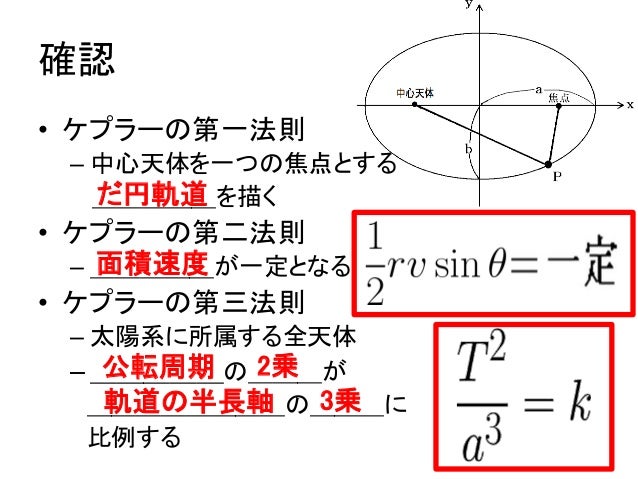
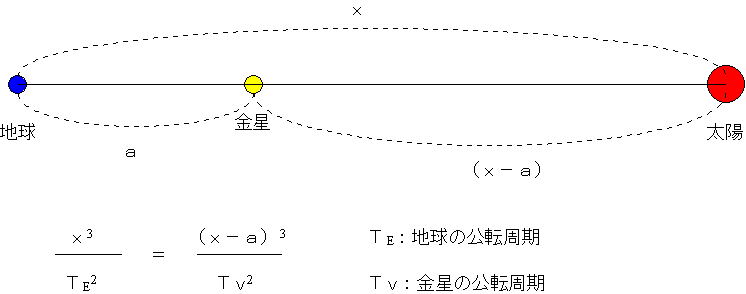
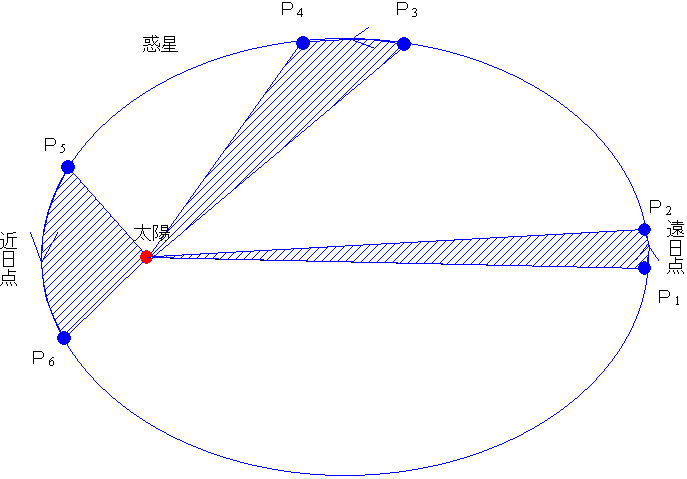
人工衛星は、地球を焦点とする楕円軌道上を運動する。これに対して、彗星の軌道には、楕円、放物線、双曲線のいずれもある。下図は、いずれも原点を焦点とする楕円、放物線、双曲線の一例である。 なお楕円の場合、楕円のつぶれ具合は離心率 という量で表され、楕円では の範囲の値をと 地球公轉的平均速度大約是298 km/s(107,000 km/h),7分鐘內就可行進12,742 km(7,918 mi),等同於地球的直徑的距離;約35小時就能行進約384,000 km(239,000 mi)的地月距離 。 在現代,地球的近日點和遠日點出現的時間分別出現於每年的1月3日和7月4日左右。 由於進動このように,万有引力のもとでの運動では,面積速度が一定であり(ケプラーの第2法則), 太陽を焦点の1つとした楕円運動が可能であり(第1法則),そのとき,周期の2乗は長軸 半径の3乗に比例している(第3法則)ことがわかる。表81 に,太陽系の9個の惑星の, 軌道と周期に関する値を

ケプラーの法則と万有引力 3つの法則をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
地球の面積速度 求め方
地球の面積速度 求め方- 地球の人工衛星同士も同じになりますが、 惑星と人工衛星では異なる値になります。 第2法則:面積速度一定の法則 惑星と太陽を結ぶ線分が単位時間当たりに描く面積(面積速度\(=\frac{1}{2}rvsin\theta\))は一定である。 第3法則:調和の法則 惑星の公転周期\(T\)と軌道長半径\(a\)は、\(T^{2}=ka^{3よって、地球の公転速度は以下のようになります。 V=(MG / R) 1/2 上記の式から判るように、地球の公転速度は 地球の質量 には 依存しません 。




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス
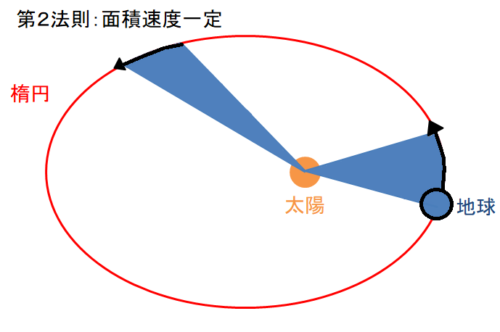
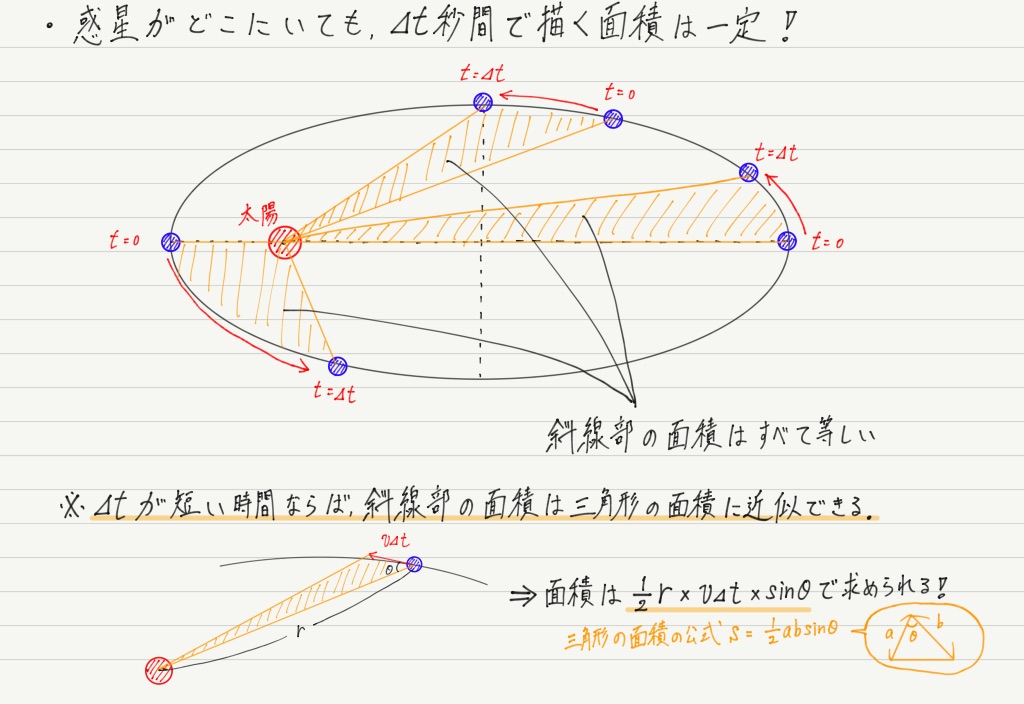
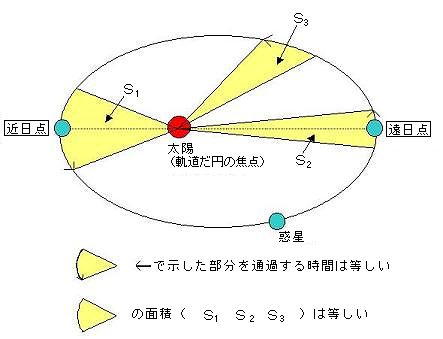
定義 面積速度とは,下図に示す が単位時間あたりに掃引する面積である. 導出 微小時間 間に,点 の座標が, から へ移動したとする. このとき, が掃引する面積を とすると, は次のように表わされる. (が十分小さいとき,)ブリタニカ国際大百科事典 小項目事典 面積速度の用語解説 動点 P が定点 O のまわりを周回運動するとき,動径 がつくる面積 S の時間変化率 dS/dt をいう。扇形速度ともいう。平面運動の場合には,点 O を原点として動点 P の極座標を (r,θ) とすれば,面積速度は次式で与えられる。惑星と太陽を結ぶ線が一定時間に描く面積(緑色の部分)は等しい。 このため太陽から近い所では速く、遠い所では遅く動きます。 面積速度一定の法則とも言います。 逆に、「面積が等しければかかる時間は等しい」「面積が大きければかかる時間は長く、小さければかかる時間は短い」とも
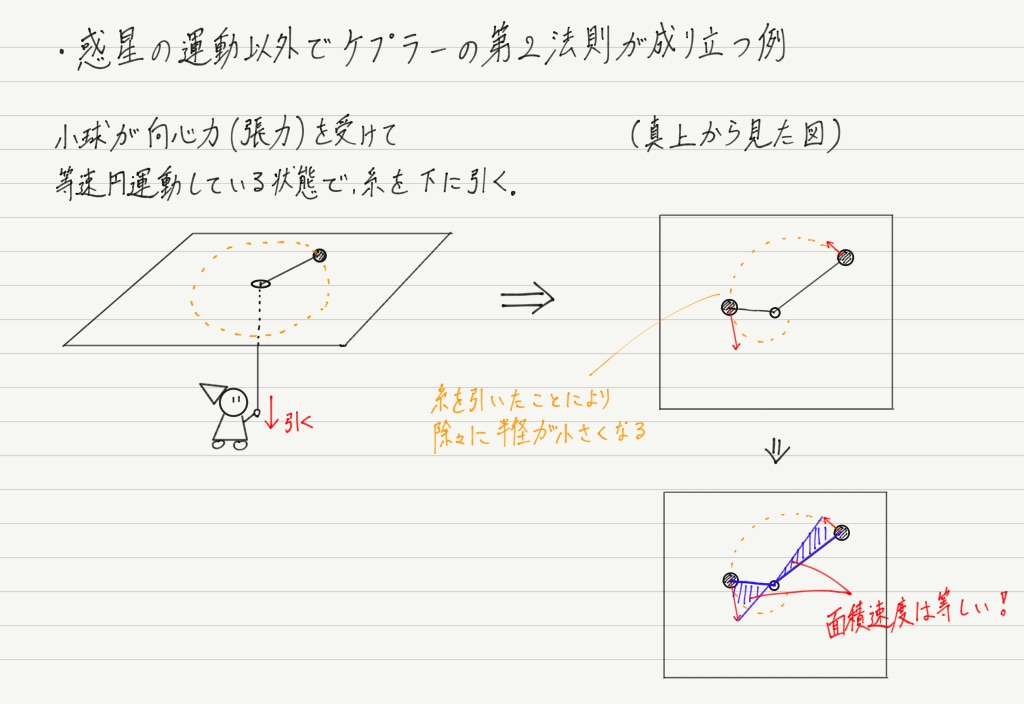
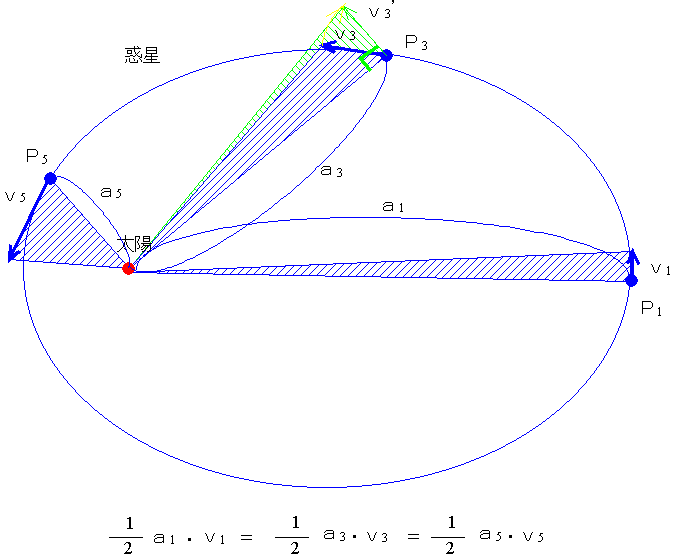
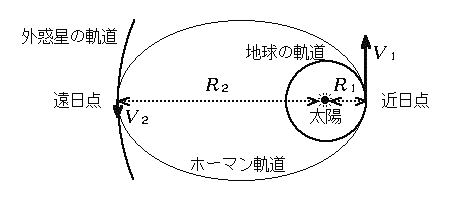
ホーマン軌道を取るときの、地球出発速度v 3 と惑星到着時の速度v 4 を角運動量保存則(面積速度一定の法則)とエネルギー保存則から求める。 ホーマン軌道については別稿 「質点の二次元運動」4.(3)(b) で述べたように以下の式が成り立つ。惑星の面積速度は各惑星ごとに一定である ケプラーの第3法則 惑星の公転周期の2乗と楕円の長半径の3乗との比は太陽系の全ての惑星について共通な一定値である これらの法則の数学的な証明は後半に回し, まずは各法則の主張を確かめることにする 後半の証明では, 証明が容易な順番に解説 この面積速度は次の式で示すことができます。 動径長さ r 、惑星の速さ ⅴ 、動径と速度がなす角度の大きさを θ 、としましょう。 そうすると図の三角形の面積が面積速度を表しています。
面積速度一定の法則ともいいます。 「太陽と惑星を結ぶ線が、一定時間に描く面積は一定である。」 では、図2を見ていきましょう。 図2 面積速度一定を示す図 ある一定時間に、惑星が楕円軌道上の点a~点bまで進んだとしましょう。 地球は、表面の約70%が海で覆われている惑星。 太陽系でただひとつ、生命が確認されており、 自身の1/4の大きさである衛星"月"を引き連れています。 スポンサーリンク 目次地球の大きさ(直径・面積・質量)ってどのくらい?またなぜ地球の回転速度が時間を経過してもほとんど変わらないのかと言うと、 それは宇宙には地球内部と違って抵抗となるものがないから です。 地球の中でボールを投げて時間が経つと動きが遅くなったり、地面に落下します。 これは地球内部ではそのボールに地球からの重力が働いてい




高校物理 ケプラーの第二法則 練習編 映像授業のtry It トライイット



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ
地球を知ろう・地球のデータ集 ぐるっと片道で世界一周ができるのは、地球が丸いから。 ・表面積 5100 656×108 km2 ・体積 10 7×1012 km3 ・質量 5972×1024 kg ・太陽との相対質量 3040 4 ×10 6乗 ・月との相対質量 ・平均密度 5514 kg/m3 ・脱出速度 km/s ・自転周期 23時間56分秒 大気圏脱出速度ってどのくらい? 地球 の重力から脱出するのに時速何万kmも出す必要が何故あるのか? と疑問に思う方が多いです。 たしかに単純に考えればジェット戦闘機くらいの 時速3,000Km あれば十分なように感じてしまいますよね。 これには 燃料面積速度一定の法則はニュートンのプリンキピアの中にもその記述・解説が見られ、ニュートンの思想に多大な影響を与えています。 この面積速度一定の法則から、角運動量保存則が導かれるのです。 ここで言う角運動量とは、質量×動径×速さ で示され



1




ケプラーの法則と万有引力 3つの法則をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ
もしかしたら、第二宇宙速度で地球を脱出した衛星はどの後どこにいくのだろう?と思っている人も多いかもしれません。 実は、第二宇宙速度で地球を離れた衛星は、次は 太陽の引力に引っ張られて太陽の周りを回る ことになります。 すると、「人口衛星」ではなく「人口惑星」という名 ケプラーの第二法則(面積速度一定の法則) 第二法則は、別名 「面積速度一定の法則」 ともいい、惑星がケプラーの第一法則の通り運動している時、 単位時間(例えば1秒や1年)で動いた距離と、 太陽を結んだおうぎ形の面積が常に同じである!と言うこと力学的エネルギー と 面積速度 です。 万有引力は保存力でなので,力学的エネルギーが保存されることは前述したとおりです。 また星Bにはたらく万有引力は常に恒星Aの方に向いています。このように力が常にある定点に向いており,かつ力の大きさが定点からの距離のみによって決まるよう



ケプラーの法則とは コトバンク



2 25 極座標の微分方程式
7–3 地球 と私たちの間 回転が2 次元的で,ある平面上に限られるとき,面積速度S は次のように表される. S = 1 2 rv ここでv は速度ベクトルの絶対値である.いま,回転する物体に働く力は中心力のみであるとき, 面積速度が一定であることを示せ. Ex 7–5 = =第2法則(面積速度一定の法則) 惑星と太陽とを結ぶ線分が単位時間に描く面積(面積速度)は、一定である。 第3法則(調和の法則) 惑星の公転周期の2乗は、軌道長半径の3乗に比例する。 先に、第1法則および第2法則が発見されて1609年に発表され 、後に、第3法則が発見されて1619年に発表さ66 第6 章 中心力のもとでの運動 面積速度 時刻t に位置r にあった質点が,微小 時間後のtΔt にrΔr に移動したとする。 微小 時間Δt のあいだに位置ベクトルが掃いた面積ΔS は,r とΔr を2辺とする三角形の面積で近似でき る(図63)。 Δr の大きさをΔr と表し,r とΔr とのなす角を



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora




高校物理 ケプラーの第三法則 映像授業のtry It トライイット
第二宇宙速度とは、その星の重力を振り切るために必要な速度です。 宇宙工学においては地球から地球外探査機を打ち上げる際によく第二宇宙速度が話題にあがるため、別名:地球脱出速度とも呼ばれます。 地球での第二宇宙速度は、約112 km/s (= 40,300 km/h )です。 円運動・万有引力 buturisya 年3月25日 / 年4月1日 円運動とは物体が円を描きながら運動をすることである。 円運動の特徴は、物体にかかる力は常に円の中心を向いていることである。 これらの円運動の例として天体の運動がある。 天体間には万有 この人工衛星の近日点と地球の中心との距離はr、遠日点と地球の中心との距離は2rとなったとき、近日点の速度は遠日点での速度の何倍になるか根拠と共に示したいんです。 ケプラーの第二法則である面積速度一定を使うと思うのですが、 示し方が良く分かりません。 宜しくお願いします。




高校物理 ケプラーの第二法則 映像授業のtry It トライイット




ケプラーの法則まとめ 理系ラボ
図101 面積速度 と表せる。万有引力は中心力なので角運動量は保存される。面積速度は角運動 量に比例するので、面積速度は一定となる。角速度は r Dq rDq 図102 面積速度一定の法則 θ˙ = L mr2 (1011) と表すことができる. x104 楕円軌道続いては、球の表面積を求める計算問題を、例題を使って解説しています。 球の表面積を求める計算問題 半径から球の表面積を求める問題 半径 3 の球の表面積 S を求めよ。 球の表面積の公式に代入すればいいだけですね。 \begin{align*} S &= 4 \pi r^2 \\5pt &= 4 \pi \times 3^2 \\5pt &= 36 \pi \\ \end{align*} 211 答え 111 時速 (km/h) を求めるので、まず365日を時間 (h) に直します。 12 時速10万キロです!




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン



3
二倍が一定、つまり面積速度が一定であることを意味する。これはケプラーの第二法則として知ら れている。 質点系 複数の質点の集まりを質点系と呼ぶ。質点系の持つ運動量ベクトルの総和が全運動量、角運動量ベクト ルの総和が全角運動量である。ベクトルと運動の法則を使って全運動量�地球の総面積は × 10 6 km 2 で、そのうち海が3622 × 10 6 km 2 (地球表面の711%)、陸地が × 10 6 km 2 (同2%)である 。 陸地は地球表面全体に均等にではなく 北半球 に偏って分布しており、陸地の多い側を 陸半球 (りくはんきゅう)、海の多い側を 水半球 (すいはんきゅう)と呼ぶ。



ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に




ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora
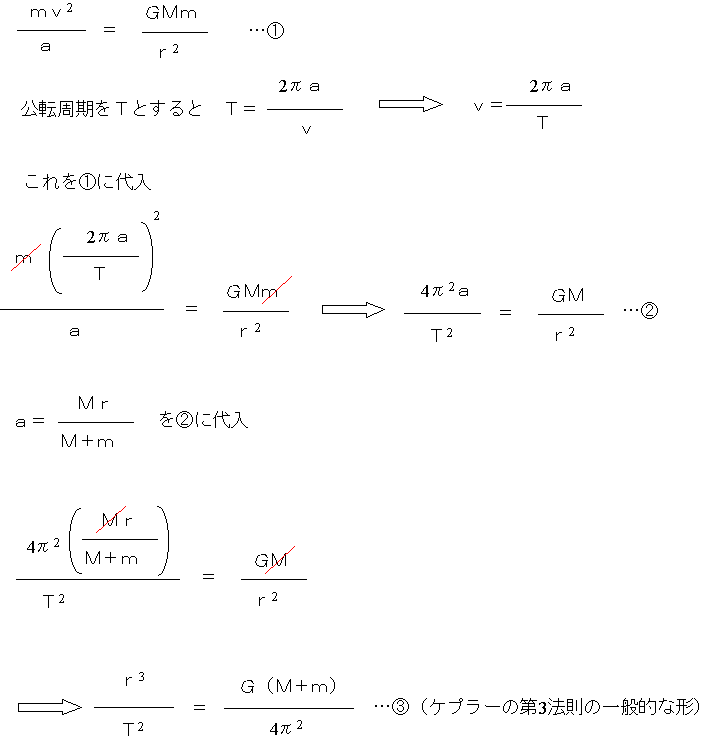



太陽系その他の天体



面積速度一定の法則っていうのは 惑星の楕円軌道でなく 地球上の Yahoo 知恵袋



ケプラーの法則



Q Tbn And9gctwwondhom4qzc3am0bbnqtx0vev1e 5dcqx6r0xfso8pxh6jg7 Usqp Cau




面積速度一定の法則 高校数学 高校化学 高校物理に関連した基礎の基礎の復習です



Http Web Tuat Ac Jp Zhang Files Hw Pdf



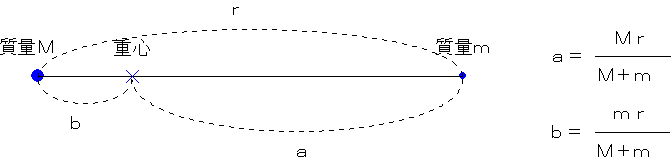
二体問題 Two Body Problem




科学のパラダイム シフト その2 2 ケプラーの第2法則 Quark Kenzo の つれづれ日記




高校物理 シンプルにまとめよう 万有引力 力学 お茶処やまと屋



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora



高校物理 元 理学部物理学科が教える ケプラーの法則 宇宙 Spacenuts




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 Study Z ドラゴン桜と学ぶwebマガジン



古典天文学



太陽系その他の天体




天文学の歴史 ケプラーの法則



ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に



第一宇宙速度より大きい初速度vを衛星に与えると楕円軌道を描いて周回運動 Yahoo 知恵袋



暦wiki ケプラーの法則 国立天文台暦計算室



Adoko 力学 ケプラーの法則




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




4 は 3 で求めた力学的エネルギーを使ってv2 の式にできますか 答えは面積速度 Clear



ケプラーの法則 わかりやすい高校物理の部屋



実験地学 10




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン




万有引力とケプラーの法則 物理の学校




高校物理 ケプラーの第二法則 練習編 映像授業のtry It トライイット



暦wiki ケプラーの法則 国立天文台暦計算室




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




高校物理 ケプラーの法則 Youtube



惑星の運動




万有引力むずい 教えてください Clear



太陽系その他の天体




ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説



太陽系その他の天体



地球や水星の面積速度の求め方は また計算に使用する固有時は Yahoo 知恵袋




中心力問題 惑星の運動や角運動量保存則 Ocean




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス
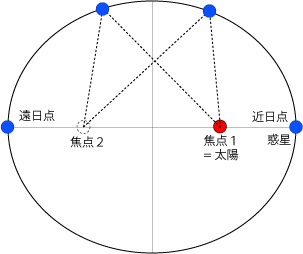



暦wiki ケプラーの法則 国立天文台暦計算室



惑星探査機の軌道と飛行速度



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ




ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説



ケプラーの第2法則 面積速度一定の法則 サラリーマン 宇宙を語る



ケプラーの法則 わかりやすい高校物理の部屋



Kakeru Movie




太陽 木星 月の質量を求める計算 惑星物理基礎ノート Planetscope



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora



物理 古典力学の基礎 惑星の運動 技術情報館 Sekigin 最も身近な惑星の運動に関連し 楕円軌道 ケプラーの法則 万有引力に項目を分けて紹介する
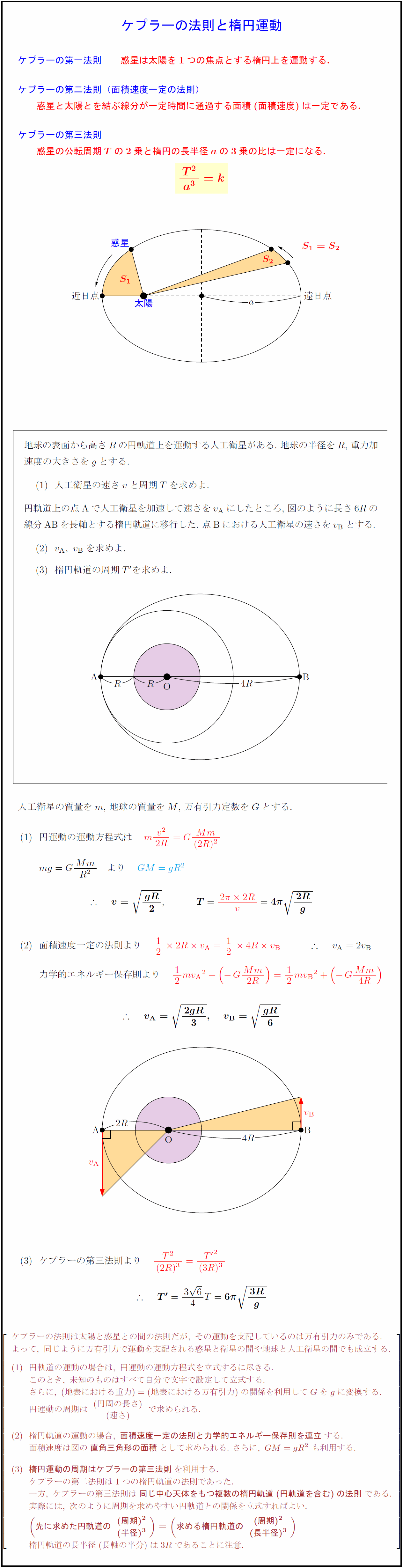



高校物理 ケプラーの法則と楕円運動 受験の月




ケプラーの法則 高校物理の備忘録
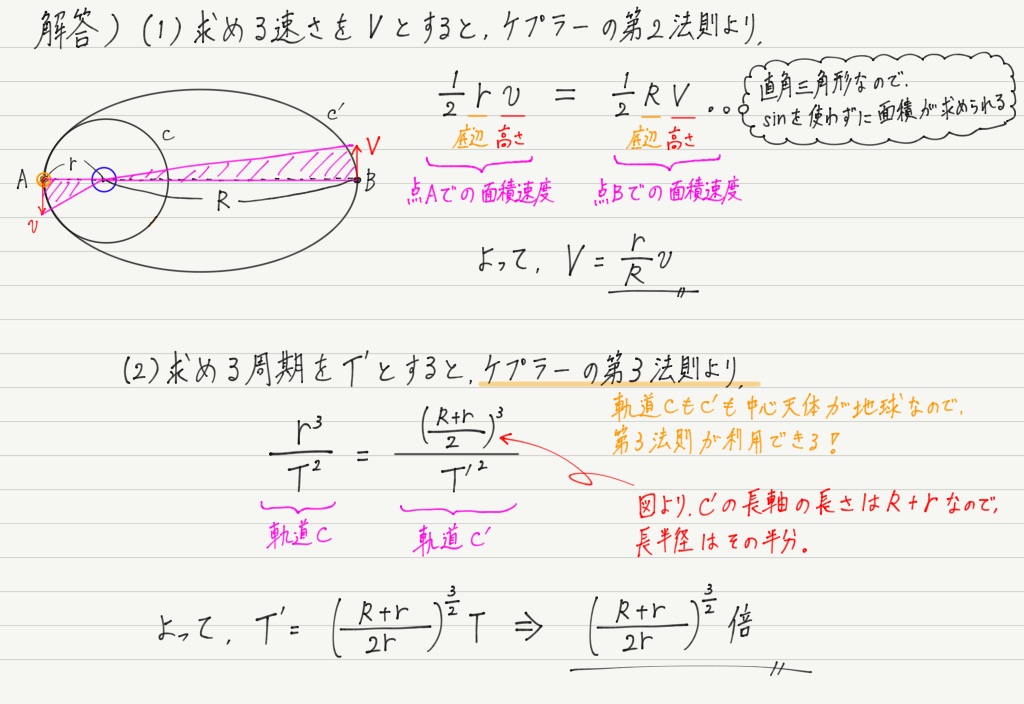



ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に




ケプラーの法則まとめ 理系ラボ




Ppt 2 1惑星と人工衛星 Powerpoint Presentation Free Download Id




4 は 3 で求めた力学的エネルギーを使ってv2 の式にできますか 答えは面積速度 Clear




太陽 木星 月の質量を求める計算 惑星物理基礎ノート Planetscope




力学 ケプラーの第二法則 面積速度一定の法則 Youtube
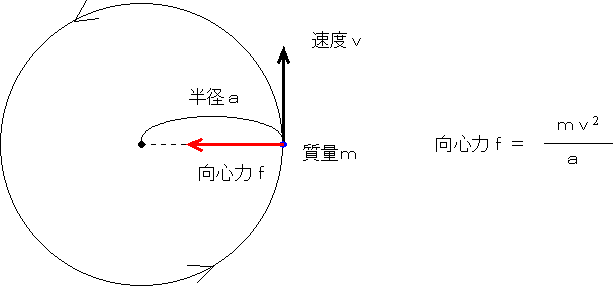



太陽系その他の天体



太陽系その他の天体



京都大学13年物理第1問 ひたすら受験問題を解説していくブログ



ケプラーの法則 近日点 遠日点 球面三角法 アナレンマ 原子時 Gmt Wut Ut Jst 時差 日時計 均時差 平均太陽時 視太陽時 標準時 地方太陽時 Yoshio S Pages 太陽 天体



Q Tbn And9gctnocnbispupw9wcbhh8rcgeqb3fc Kw21fmrehorpde36zoh Usqp Cau




太陽系その他の天体




ケプラーの法則 Wikipedia
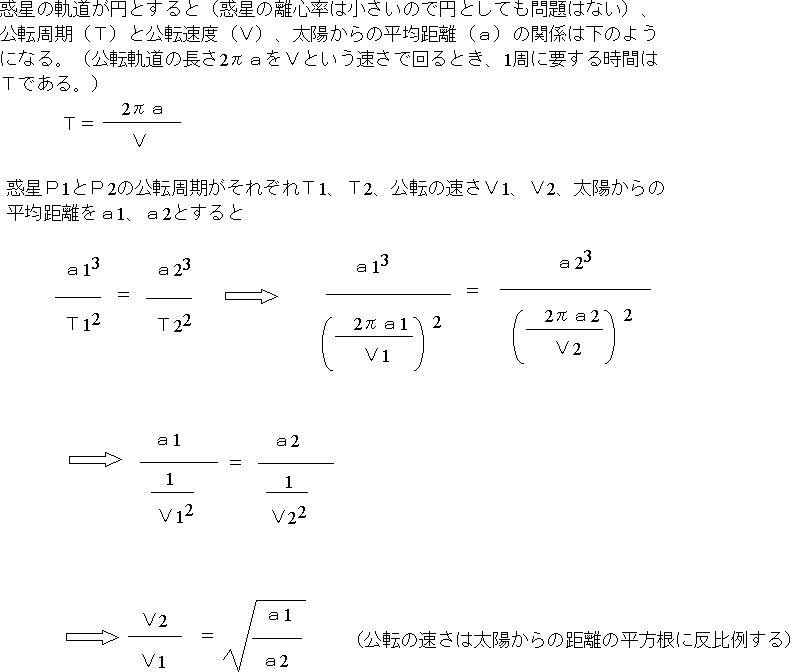



太陽系その他の天体



Www Hiragaku Ac Jp Challenges Kakonokadai 413 424 Pdf 4 21 4 E6 9c 81 E6 97 A5 E9 85 8d E4 Bf A13 E5 B9 B4 E9 80 B2 E5 Ad A6 E7 90 86 E7 4 E7 B5 84 E7 E7 90 86 Pdf



ケプラーの法則




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




ケプラーの法則 高校物理の備忘録




地球 Wikipedia



ケプラーの第2法則についての疑問です 下図は名問の森42のqの問題と解説で Yahoo 知恵袋




ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に



太陽ってどんな星



古典天文学




ケプラーの法則とハレー彗星 Koko物理 高校物理



太陽系その他の天体



面積速度一定の法則 高校数学 高校化学 高校物理に関連した基礎の基礎の復習です




ケプラーの法則 高校物理の備忘録




ケプラーの法則とハレー彗星 Koko物理 高校物理



ケプラーの法則 わかりやすい高校物理の部屋



Www Tsuyama Ct Ac Jp Imgver4 Kyousyokuin Kiyou Kiyou18r03 Pdf



ケプラーの第二法則 面積速度一定の法則 の求め方




高校物理 以外に難しいケプラーの法則の使い方 月と水星は ハレー彗星は 物理参考書執筆者 プロ家庭教師 稲葉康裕 Coconalaブログ




112番で解答の等式 の部分が1になるのはなぜですか Clear
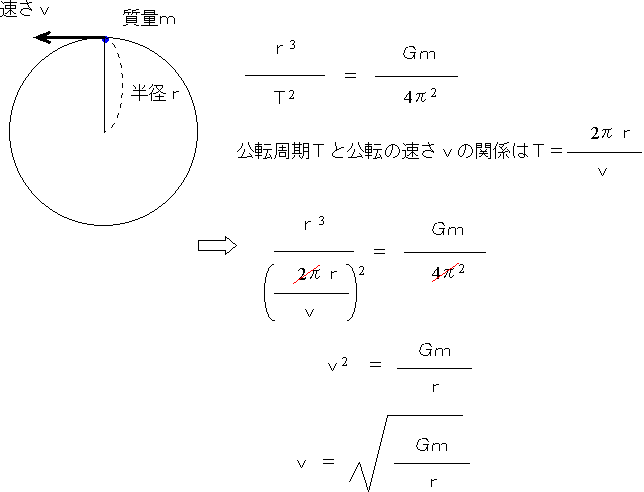



太陽系その他の天体




高校物理 シンプルにまとめよう 万有引力 力学 お茶処やまと屋



学生読み物 人工天体の運動学




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス



惑星探査機の軌道と飛行速度



0 件のコメント:
コメントを投稿